Solving a 4x4 Rubik's Cube, also known as the Rubik's Revenge, is an exciting challenge that builds on the fundamentals of the standard 3x3 cube but introduces additional complexity. When Nomads have their free time, let's enjoy it. However, most beginners can usually give up. Therefore, understanding the notation is crucial for learning and communicating the sequences of moves necessary to solve it. This guide will help you grasp the notation rules used in solving a 4x4 Rubik's Cube.
Table of Contents
Introduction to the 4x4 Rubik's Cube
Differences from the 3x3 Cube
The 4x4 Rubik's Cube adds an extra layer of complexity compared to the 3x3 cube. It has 16 smaller squares on each face, totaling 96 smaller squares compared to the 54 on a 3x3 cube. The additional center pieces and edge pairs introduce new challenges and require a more advanced notation system.

Importance of Notation
Notation is the language of Rubik's Cube solving. It allows you to record and share algorithms (sequences of moves) that manipulate the cube in specific ways. Accurate notation is essential for learning and executing algorithms correctly.
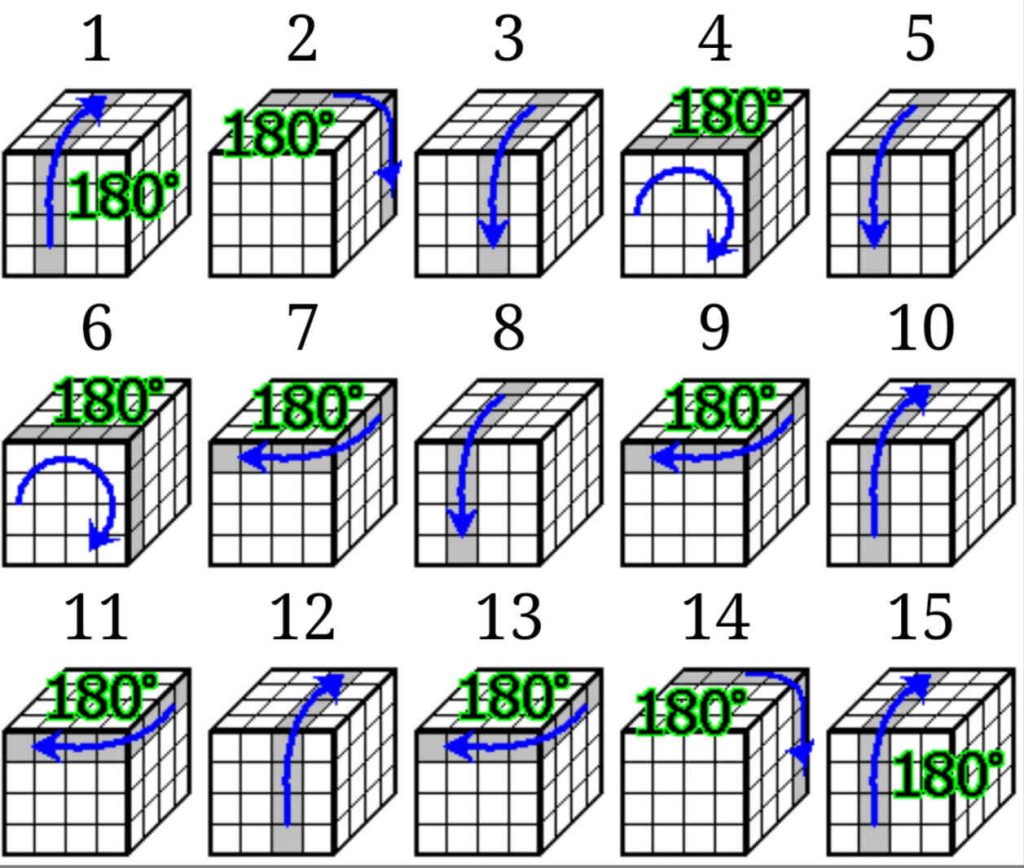
Basic Notation
Faces and Turns
The 4x4 cube uses the same face notation as the 3x3 cube, with each face represented by a letter:
- U: Up face
- D: Down face
- L: Left face
- R: Right face
- F: Front face
- B: Back face
Types of Turns
- Single Face Turns: A letter by itself (e.g., U, D, L, R, F, B) indicates a 90-degree clockwise turn of that face.
- Counterclockwise Turns: A letter followed by an apostrophe (e.g., U', D', L', R', F', B') indicates a 90-degree counterclockwise turn of that face.
- 180-Degree Turns: A letter followed by a 2 (e.g., U2, D2, L2, R2, F2, B2) indicates a 180-degree turn of that face.
Advanced Notation for 4x4 Cube
Inner Slice Moves
The 4x4 cube has inner slice moves, which are not present in the 3x3 cube. These are the middle layers between the outer faces.
- Uw: Upper wide turn, both the outer U layer and the inner slice turn together clockwise.
- Dw: Down wide turn, both the outer D layer and the inner slice turn together clockwise.
- Lw: Left wide turn, both the outer L layer and the inner slice turn together clockwise.
- Rw: Right wide turn, both the outer R layer and the inner slice turn together clockwise.
- Fw: Front wide turn, both the outer F layer and the inner slice turn together clockwise.
- Bw: Back wide turn, both the outer B layer and the inner slice turn together clockwise.
Inner Slice Specific Moves
These moves involve only the inner slices without affecting the outer layers.
- u: Upper inner slice move, the inner layer adjacent to U, turns clockwise.
- d: Down inner slice move, the inner layer adjacent to D, turns clockwise.
- l: Left inner slice move, the inner layer adjacent to L, turns clockwise.
- r: Right inner slice move, the inner layer adjacent to R, turns clockwise.
- f: Front inner slice move, the inner layer adjacent to F, turns clockwise.
- b: Back inner slice move, the inner layer adjacent to B, turns clockwise.
Example Algorithms
Edge Pairing
One of the essential steps in solving the 4x4 cube is pairing the edges. Here's a simple algorithm to swap edges:
- Uw' Lw' U' Lw Uw Lw U Lw'
- This algorithm pairs edges by manipulating the top and left layers. Each letter represents a move as described in the notation rules above.
Solving the Centers
Solving the centers is a crucial step in solving the 4x4 cube. Here's a helpful algorithm to move center pieces:
- Rw U Rw' U' Rw' F Rw2 U' Rw' U' Rw U Rw' F'
- This algorithm helps in rearranging the center pieces to form a solid color on each face.
Parity correction
- l2 B2 r F'2 l'
- F'2 U'2 l' U'2 l
- U'2 r' U'2 B2 l2
Practice Tips
Learn and Practice Basic Algorithms
Start with the basic algorithms and practice them until you can perform them without thinking. Understanding these basics is crucial before moving on to more complex sequences.
Visualize Moves
Use a physical cube or a digital simulator to visualize each move. Seeing how each turn affects the cube helps in understanding the notation and the resulting changes.
Break Down Algorithms
Break down longer algorithms into smaller parts and practice each part individually. This approach makes it easier to memorize and execute complex sequences.

Conclusion
Mastering the notation of a 4x4 Rubik's Cube is essential for solving it efficiently. By understanding the faces, types of turns, and specific moves unique to the 4x4 cube, you can follow and develop algorithms to solve this fascinating puzzle. Regular practice and familiarizing yourself with the notation will significantly improve your solving skills.
Happy cubing!

